$Математика$	Основы радиоэлектроники и связи
3. Линейные цепи при произвольных воздействиях : 3.2. Частотный метод анализа

3.2.4 Простейшие фильтры первого порядка

К простейшим фильтрам первого порядка относятся цепочки, содержащие активные сопротивления и один реактивный элемент: емкость или индуктивность, включенные последовательно или параллельно. На рис.6 изображены возможные включения элементов R и L, R и C.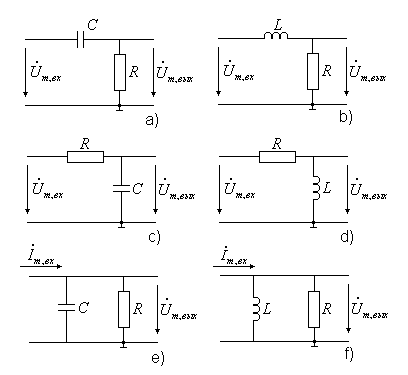

Рис. 6

Цепочки вида a), b), c), d) питаются от источника напряжения, а цепочки вида e) и f) – от источника тока.

Для определения фильтрующих свойств этих цепочек, запишем для каждой из них частотный коэффициент передачи, причем для цепочек a), b), c), d)

а для цепочек e), f)

, – комплексные амплитуды входных напряжений и тока, -комплексная амплитуда выходного напряжения. Коэффициенты передачи определим для случая холостого хода на выходе ().

Для определения коэффициентов передачи цепочек воспользуемся комплексным методом, при котором гармонические токи и напряжения представляем их комплексными амплитудами (), емкость и индуктивность их комплексными сопротивлениями:

Покажем вывод коэффициента передачи на примере цепочки вида а).

Ток, протекающий в цепи в соответствии с 2-м законом Кирхгофа и законом Ома равен

в свою очередь выходное напряжение равно

Откуда получаем следующее выражение для частотного коэффициента передачи этой цепочки:

;

Аналогично легко вывести и коэффициенты передачи для других цепочек

;

;

;

;

.

Обозначим : RC=t _ц, L/R=t _ц, где t _ц - постоянная времени цепи, = , где - граничная частота цепочки.

Получаем для цепочек a) и d) коэффициент передачи вида:

для цепочек b) и c):

и для цепочек e) и f) соответственно :

Сравнивая соотношения для коэффициентов передачи всех цепочек, можно заметить, что все цепочки можно разделить на 2 вида, коэффициенты передачи которых можно записать следующим образом:

причем в последовательных цепочках , а в параллельных ,

Для построения графиков АЧХ и ФЧХ и оценки фильтрующих свойств цепочек первого порядка рассмотрим следующие области частот: область низких частот , область высоких частот и .

Для первого типа цепочек имеем:

В области низких частот поэтому

Таким образом, в области низких частот для первого типа цепочек (a, d, f) АЧХ линейно возрастает от нуля, т.е. наклон АЧХ здесь составляет 6 дб/октаву: увеличение в 2 раза частоты увеличивает в 2 раза модуль коэффициента передачи, а ФЧХ примерно равна p /2.

На частоте модуль коэффициента передачи

Отсюда и название этой частоты –“граничная”; эта частота определяет полосу пропускания фильтра по уровню K₀/Ц2.

В области высоких частот

т.е. в области высоких частот цепочки первого типа имеют равномерную АЧХ, равную K₀ ; а у цепочки второго типа модуль АЧХ с увеличеним частоты изменяется по закону , т.е. имеет наклон -6 дб/октаву, ФЧХ в этой области примерно равна -p /2. На рис.7 представлены графики АЧХ и ФЧХ обоих типов цепочек.

Рис. 7

Таким образом, простейшие апериодические цепочки порядка первого типа (вида a, d, f рис.6) являются фильтрами высокой частоты со спадом частоты АЧХ вне полосы пропускания (, ) 6 дб/октаву; простейшие цепочки второго типа (b, c, e) являются фильтрами низких частот со спадом АЧХ вне полосы пропускания (0,) также в 6 дб/октаву. Граничная частота здесь определяется по уровню пропускания половинной мощности или по спаду АЧХ на 3 дб от максимума.