4.5.1 Постановка задачи оптимального приема
Одной из задач радиотехники является задача
обнаружения сигнала на фоне помехи. На вход системы, решающей эту задачу,
поступает колебание  ,
которое при отсутствии сигнала представляет собой шум ,
которое при отсутствии сигнала представляет собой шум  ,т.е. ,т.е.
 , а
при наличии сигнала в простейшем случае сумму сигнала и шума: , а
при наличии сигнала в простейшем случае сумму сигнала и шума:

Таким образом сигнал на входе приемника можно
записать в следующем виде

где  ,
если сигнала нет (обозначим этот случай ,
если сигнала нет (обозначим этот случай  )
и )
и  ,
если он есть (случай ,
если он есть (случай 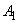 ). ).
Величина  заранее неизвестна и её надо определить. Из-за случайного характера шума
или помехи при решении задачи обнаружения возможны ошибки. Если приемник
решает, что
заранее неизвестна и её надо определить. Из-за случайного характера шума
или помехи при решении задачи обнаружения возможны ошибки. Если приемник
решает, что  ,
будем считать, что это случай ,
будем считать, что это случай  ,а
если ,а
если  ,то
случай ,то
случай  .
При этом возможны четыре варианта решения: .
При этом возможны четыре варианта решения:
- сигнала нет, и приемник определяет, что
его нет – правильное необнаружение сигнала (ситуация
 )
; )
;
- сигнала нет, а приемник определяет, что
он есть – ошибочное обнаружение сигнала, ложная тревога (ситуация
 ); );
- сигнал есть, и приемник определяет, что
он есть – правильное обнаружение (ситуация
 ); );
- сигнал есть, а приемник определяет, что
его нет – пропуск сигнала (ситуация
 ). ).
Наиболее просто решается задача обнаружения
полностью известного сигнала. Задача усложняется, чем больше случайных
неизвестных параметров (или характеристик) имеет обнаруживаемый сигнал.
В этом случае сигнал описывается не просто функцией времени, но и функцией
случайных параметров  ,
где ,
где  -матрица
параметров сигнала. Еще более сложной оказывается задача разрешения нескольких
сигналов. В этом случае на входе приемника действует сигнал -матрица
параметров сигнала. Еще более сложной оказывается задача разрешения нескольких
сигналов. В этом случае на входе приемника действует сигнал  ,
представляющий собой сумму помехи ,
представляющий собой сумму помехи  и двух возможно налагающихся сигналов
и двух возможно налагающихся сигналов  и
и  ,
т.е. ,
т.е.

где 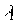 и и -случайные
величины, которые могут принимать значения 0 или 1. Если сигналы не являются
полностью известными, то встает задача разрешения сигналов со случайными
параметрами: -случайные
величины, которые могут принимать значения 0 или 1. Если сигналы не являются
полностью известными, то встает задача разрешения сигналов со случайными
параметрами:  ; ;
В понятие “разрешить два сигнала” можно вкладывать
различный смысл. При возможности одновременного наличия в принятой реализации
 двух
сигналов, можно иметь в виду только раздельное обнаружение сигналов с
заданными показателями, а можно не только раздельное обнаружение, но и
определение какого-либо параметра a i .
Так, если показатели обнаружения второго сигнала остаются выше допустимых
в присутствии случайного первого сигнала, то можно говорить, что второй
сигнал разрешается в смысле обнаружения (оценки параметра двух
сигналов, можно иметь в виду только раздельное обнаружение сигналов с
заданными показателями, а можно не только раздельное обнаружение, но и
определение какого-либо параметра a i .
Так, если показатели обнаружения второго сигнала остаются выше допустимых
в присутствии случайного первого сигнала, то можно говорить, что второй
сигнал разрешается в смысле обнаружения (оценки параметра  ).
Если в дополнение к этому разрешается и первый сигнал при наличии второго,
то можно говорить, что сигналы взаимно разрешаются в смысле обнаружения
(оценки параметра ).
Если в дополнение к этому разрешается и первый сигнал при наличии второго,
то можно говорить, что сигналы взаимно разрешаются в смысле обнаружения
(оценки параметра  ).
Математической базой для решения всех задач приема сигналов, связанных
с риском ошибок принятия решения о наличии сигнала при его отсутствии,
и пропуск сигнала, является теория вероятностей и математической статистики,
при этом обеспечивается возможность учета не только информации о принятом
колебании, но и априорных сведений относительно сигнала и помех. ).
Математической базой для решения всех задач приема сигналов, связанных
с риском ошибок принятия решения о наличии сигнала при его отсутствии,
и пропуск сигнала, является теория вероятностей и математической статистики,
при этом обеспечивается возможность учета не только информации о принятом
колебании, но и априорных сведений относительно сигнала и помех.
|