Основы радиоэлектроники и связи

13. Воздействие случайных сигналов на нелинейные цепи : 13.1. Преобразование случайного процесса в безинерционных нелинейных элементах

13.1.3 Воздействие гауссовского процесса на нелинейный элемент с кусочно-линейной
аппроксимацией

Линейно-ломанную аппроксимацию характеристики нелинейного элемента можно описать следующим образом:

где S – наклон (крутизна) характеристики.

В соответствии с (2) для процесса с нормальным распределением имеем

В точке у=0 при любых неотрицательных значениях х вероятность Р(у=0) равна вероятности того, что х<0, которая равна 1/2. Следовательно плотность вероятности р(у=0)=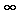 . Это обстоятельство можно учесть добавлением к выражению для р(у) члена вида при у>0. Это слагаемое везде, кроме точки у=0 равно нулю. При интегрировании это слагаемое дает 1/2. Графики р(х) изображены на рис.3.

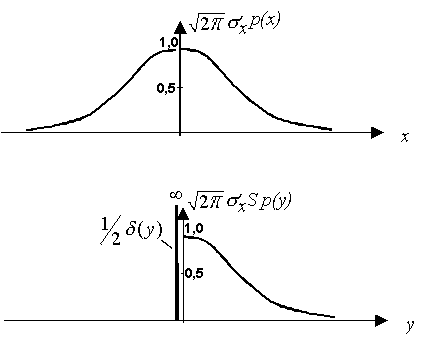
Рис.3.

Если кусочно-линейная характеристика имеет также и участок насыщения у₀, то плотность вероятности р(у) в этом случае ограничена двумя дельта-функциями при у=0 и у=у₀ (см. рис.4). Этот случай характерен для ограничителей сигнала.

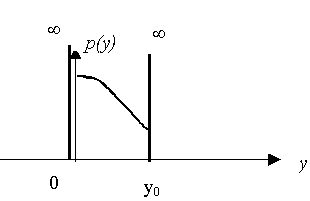
Рис.4.

Рассмотренный способ определения вероятностных характеристик сигнала на выходе нелинейного элемента не учитывает влияние выходных цепей, которые, как правило, являются частотно-зависимыми.

© Андреевская Т.М., РЭ, МГИЭМ, 2004