Основы радиоэлектроники и связи

5. Основы синтеза линейных цепей : 5.3. Синтез четырехполюсников

5.3.3 Синтез фильтров нижних частот

Идеальный фильтр нижних частот с полосой прозрачности w _пр имеет АЧХ вида рис.11.

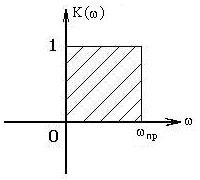
Рис. 11

По виду полинома знаменателя передаточной характеристики различают фильтры Баттеворта, Чебышева, Золотарева, Бесселя и др.

1. Фильтры Баттеворта.

   Квадрат АЧХ фильтра Баттеворта имеет вид:

   ,                                                            (1)

   где – нормированная частота, e – параметр, определяющий максимальное затухание на границе полосы пропускания, n – порядок фильтра. График функции К(W ) для разных n показан на рис. 12.

   

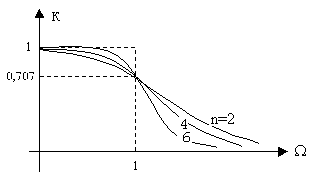
   Рис. 12

   В полосе пропускания коэффициент передачи меняется монотонно. Такая аппроксимация называется максимально плоской. Операторная характеристика фильтра получается из квадрата АЧХ:

   

   Полюса передаточной характеристики равны где k = 1, 2, …, n – для четных n, и , k=0, 1, 2 (n-1) – для нечетных n. Таким образом, полюса располагаются на окружности единичного радиуса, а разность аргументов соседних корней равна . На рис.13 показаны полюса для n=1, 3, 4.

   

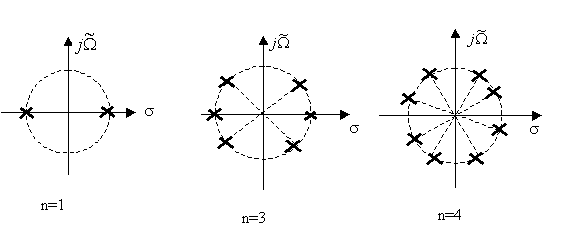
   Рис. 13

   Вид функции К(р) и расположение полюсов не зависят от величины e .

   С увеличением порядка фильтра n его АЧХ вне полосы пропускания спадает все более круто. Полоса же пропускания не зависит от порядка фильтра.

2. Фильтры Чебышева.

   Аппроксимация АЧХ фильтра производится здесь по формуле

     ,

   где при ; при W >1 – полином Чебышева.

   Графики функции К(W ) для n=2 и n=4 приведены на рис. 14. Такая аппроксимация называется равноволновой. Границы колебания АЧХ внутри полосы пропускания задаются величиной e .

   

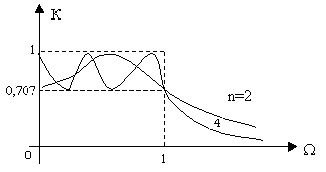
   Рис. 14

   Операторные передаточные функции фильтров Баттеворта и Чебышева имеют одинаковый вид

   

   и различаются лишь значениями полюсов. Фильтры с такой характеристикой называют полиномиальными. Пример схемы ФНЧ полиномиального типа изображен на рис. 15.

   

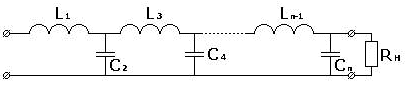
   Рис. 15

   При одинаковых требованиях к ФНЧ фильтры Чебышева требуют меньшего порядка, чем фильтры Баттеворта, однако последние вносят меньшие искажения.

3. Фильтры Золотарева.

Название таких фильтров происходит от названия дробей Золотарева, используемых для описания передаточной функции фильтра, которая представляет собой отношение двух полиномов, нули которых располагаются так, чтобы К(W ) в полосе задержания имела минимумы (см.рис.16).

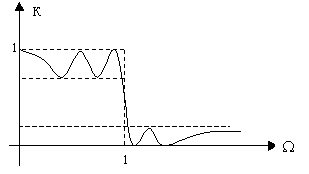
Рис. 16

Порядок фильтра Золотарева и его сложность самые минимальные. Часто эти фильтры называют эллиптическими, так как они требуют для своего описания эллиптические функции. На рис.17 приведен пример схемной реализации ФНЧ Золотарева.

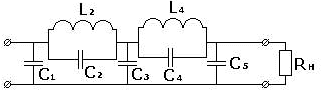
Рис. 17

© Андреевская Т.М., РЭ, МГИЭМ, 2004